#234 石川ら(2008)の追試験
投稿#232では、重量単価設定における再現性と客観性を担保するために、既存統計を利用する有用性について言及しました。
次いで、投稿#233では、橘ら(2012)とは異なる手法で重量単価を設定した先行研究(以下、「石川ら(2008)と表記)についてご紹介しました。
今回の投稿は、石川ら(2008)の追試験についてです。
重量単価推計対象の部門
石川ら(2008)は、表1に示す15(列)部門を選び、生産者価格百万円当たりの製品重量の推計対象としました。
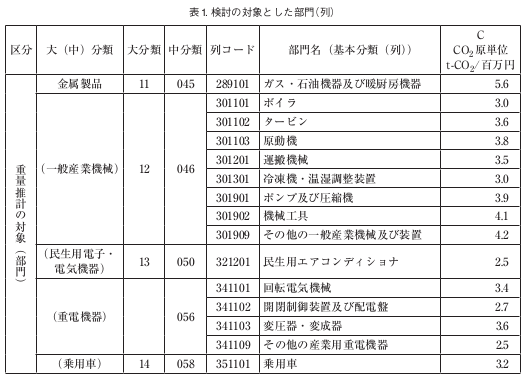
表 1. 検討の対象とした部門(列)(石川ら(2008)より引用
そして、各部門の生産者価格百万円当たりの対象部門の製品重量(重量原単位)M(t/百万円)を原材料となる中間投入(行)部門の重量原単位M(t/百万円)から求めています。
ここで石川ら(2008)がいうところの重量単位M(t/百万円)は、本ブログでいうところの「重量単価(t/百万円)」と一致します。
素材重量と産業連関表による製品重量の算出
表 1に示した 15(列)の対象部門の重量原単位 M(t/百万円)を算定するために、石川ら(2008)は、産業連関表の大分類について、表2のとおり整理を行いました。

表 2. 重量推計の中間投入とした部門(大分類)(石川(2008)より引用)
表 2において対象区分に○をつけた部門は対象部門の製品重量に反映する原材料および中間製品となる部門と考えた。また、×をつけた部門は対象部門品となる部門と考えた。また、×をつけた部門は対象部門については、対象部門の原材料であるか否かが不明な部門と考えた。
(石川ら(2008)より引用)
表2のように中間投入を整理した上で、石川ら(2008)は、中間投入となる全ての関連部門(素材および中間製品)について、重量原単位M(t/百万円)を求めることとしました。
中間投入のうち、製品の金属部分の中間投入については、表3に示しています。
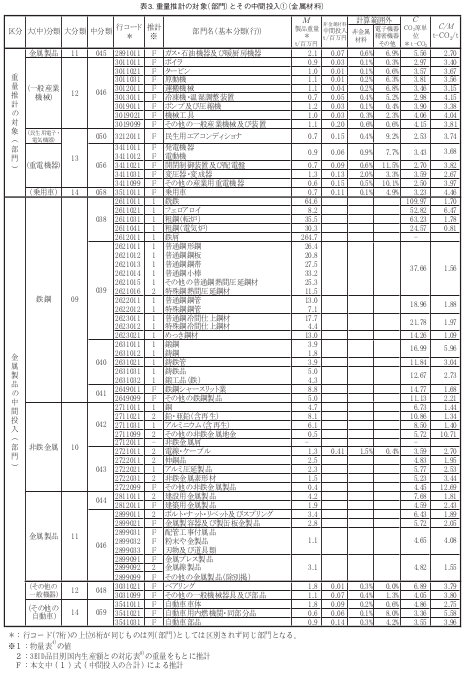
表 3. 重量推計の対象(部門)とその中間投入①(金属材料)(石川ら(2008)より引用)
また、金属以外の素材の中間投入については、製品重量との関係が明確でない場合もあるので、重量への反映については、表 4に示すように、個別に検討を行っています。
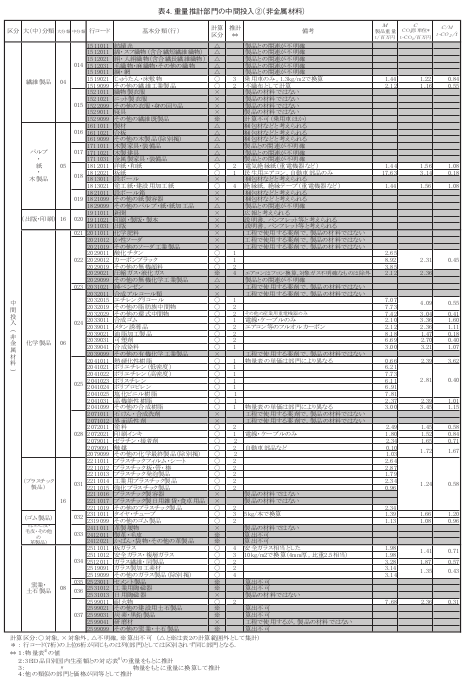
表 4. 重量推計部門の中間投入②(非金属材料)(石川ら(2008)より引用)
上記の表 3、表 4以外で、表 2において重量推計の対象部門の中間投入となる部門は、(13)電気機械のうち電子機器・通信機器等および(14)精密機械であるが、これらの部門は産業連関表(物量表)や 3EIDから製品の重量原単位 M(t/百万円)を求めることがやや困難な部門であり、対象部門の製品重量に占める割合が少ないと考えられるため計算対象から除外した。
表3に示す鉄鋼、非鉄金属(銅、アルミニウム等)および金属製品(産業連関表の大分類による)のうち、2000年度産業連関表の付属表である物量表に記載のある 23
部門(行)については、物量表の製品重量データと生産額から重量原単位 M(t/百万円)を求めた。また、物量表に記載のない金属材料や製品のうち、9部門(行)については、3EID品目別国内生産額との対応表に列部門の内訳となる製品の(一部または全部の)重量の記載があるので、行部門に対応する製品の生産数量と生産額から加重平均により重量原単位を求め、これを該当部門の重量原単位 M(t/百万円)とした。
表4に示す非金属材料についても、表 3と同様に物量表または 3EID品目別国内生産額との対応表をもとに重量原単位M(t/百万円)を計算した。また、重量以外の数量データが得られている部門はこれを製品の代表的な単位重量データ(推定値を含む)により、重量原単位M(t/百万円)に換算した。なお、これらの方法によっても重量が推計できない部門(表4計算区分:※)および対象であるか否かが不明確な部門(表4計算区分 :△)については、計算対象外とした。これらを除外した表 4の計算対象部門(計算区分:○)は 43部門(行)である。
(石川ら(2008)より引用)
表 3、表4の合計 75部門(行)の重量原単位 M(i)(t/百万円)をもとに、対象部門の中間投入(行部門)となる金属製品および中間製品のうち重量原単位が不明な15部 門( 行 ) と、15部門( 列 )の対象部門について、百万円あたりの製品重量(重量原単位)M(j)(t/百万円)を、石川ら(2008)は、次式によって計算しました。(i=行番号、j=列番号)
$$
\begin{gather} M(j) =\frac{\sum_{i}M(i) \times 中間投入額(i, j) - WF(j)}{生産額(j)}[t/10^6yen] \label{eq:1} \end{gather}
$$
WF(j):物量表による列部門jにおける屑鉄の重量(t)
(1)式において、対応する行部門は 75+15+15=105 行であるが、前述のとおり 75行の M(i)は定数である。次に中間投入となる重量原単位が不明な 15部門(行)の M(i)については行・列の不整合のため、一部の部門を集約し、対応する 12部門(列)として M(j)を計算し、その結果を対応する行部門の M(i)に代入している。ただし、M(j)のうち、鉄屑として回収される廃材分の重量 WF(j)は差引いている。以上により、関係式(1)は、12+15=27部門(列)の M(j)の連立一次方程式となる。ここでは、表計算ソフトによる収束計算を利用して、M(j)の値を求めた。
(石川ら(2008)より引用)
本ブログでは、表計算ソフトではなく、Pythonの最適化ライブラリであるPyomoおよびソルバーIpoptを利用して、M(j)の値を求めました。
以下に、Pythonのコードを記述します。
関係式(1)を解くコード
# 連立一次方程式を立式し、収束計算によってMiを算出する
import pyomo.environ as pyo
# ConcreteModelクラスを用いて問題のオブジェクトを作成
model = pyo.ConcreteModel()
# リストで指定した内容をキーワードとして保持
df_x_index = df_h12_var_x.index
NUMj = len(df_x_index)
model.x_ITEMS = list(df_x_index)
xx = {df_x_index[j]: df_h12_var_x.iat[j, 1] for j in range(NUMj)}
def initializeX(model, j):
'''変数の初期化'''
return xx[j]
model.x = pyo.Var(model.x_ITEMS, domain=pyo.PositiveReals, initialize=initializeX)
# 変数27部門(列)のM(j)を中間投入表に代入
for ccode in model.x_ITEMS:
for rcode in df_h12_MIi.index:
if rcode.startswith(ccode):
df_h12_MIi.loc[rcode, 'Mi'] = model.x[ccode]
# 目的関数を定義
model.OBJ = pyo.Objective(sense = pyo.minimize)
# 制約条件を定義
model.CONST = pyo.ConstraintList()
for ccode in model.x_ITEMS:
# .item()または.values[0]を使用してスカラー値を取得
pj = df_h12_Pj.loc[ccode, 'Pj'].item() # 生産額
wfj = abs(df_h12_WFj.loc[ccode, 'WFj'].item()) # 鉄屑として回収される廃材分の重量WF(j)
summi = 0
for rcode in df_h12_MIi.index:
if (ccode, rcode) in df_h12_io.index:
val = df_h12_MIi.loc[rcode, 'Mi'] * df_h12_io.loc[(ccode, rcode), 'price'].values[0]
if not pd.isna(val):
summi += val
model.CONST.add(model.x[ccode] == (summi - wfj) / pj)
# ソルバーのインスタンスを作成し、optに代入
opt = pyo.SolverFactory('ipopt')
# 計算のログ出力の詳細度合い (print_level) を設定
opt.options["print_level"] = 4
res = opt.solve(model, tee=True) # 計算を実行
# 計算結果を表示
for j in model.x_ITEMS:
print(f"x{j}: {model.x[j].value:.1f}")
出力結果は、以下のようになります。
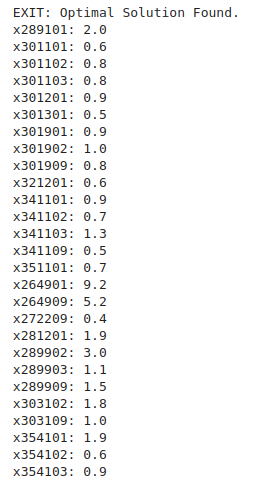
計算結果の出力画面の一部を表示
石川ら(2008)の結果と追試験の結果との比較
石川ら(2008)と今回実施した追試験の結果を比較します。
X軸に、石川ら(2008)の結果の値を、Y軸に上記の出力結果を取り、散布図を描画します。
また、XとYの相関係数の産出も行います。
散布図の描画と相関係数の算出を行うコードは、以下のようになります。
石川ら(2008)の結果と追試験の結果との比較を行うコード
# 石川ら(2008)との比較を行う
# 重量単価を小数点第1位に丸める
df_h12_solved.round({'Mj': 2},)
# 石川ら(2008)の結果のCSVファイルをDataFrameに読み込む
df_h12_table1 = pd.read_csv('h12table1.csv')
ccodetoindex(df_h12_table1)
# 散布図の描画
fig, ax = plt.subplots(1, 1)
t_x = df_h12_table1['M']
t_y = df_h12_solved['Mj']
# 散布図の描画
data = pd.DataFrame({'x':t_x, 'y':t_y})
ax.scatter(data.x, data.y)
# 直線y=xの描画
max_x = max(t_x)
max_y = max(t_y)
max_int = int(max(max_x, max_y) + 1 )
plt.plot([0, max_int], [0, max_int], color='red')
# 相関係数の算出
correlation = np.corrcoef(t_x, t_y)
print("相関係数:" + str(correlation[0,1]))
# グラフタイトルの入力
fig.suptitle('Relationship between the weight per unit price in the follow-up experiment and the result of Ishikawa et al.,2008')
# 軸ラベルの入力
ax.set_xlabel("the weight per unit price from Ishikawa et al.,2008")
ax.set_ylabel("the weight per unit price from the follow-up experiment")
# X軸の範囲を設定
ax.set_xlim([0, max_int])
# Y軸の範囲の設定
ax.set_ylim([0, max_int]);
# 目盛り線の描画
ax.grid(which='major', axis='x', color='black', linestyle='--', linewidth=1)
ax.grid(which='major', axis='y', color='black', linestyle='--', linewidth=1)上記のコードを実行するした結果は、以下のようになります。

図1. 石川ら(2008)の結果と追試験の結果との比較
得られた相関係数が0.9を超えているので、高い精度の追試験が実施できたと考えています。
引用文献
石川 明, 加藤 丈佳, 鈴置 保雄, 産業連関表を用いた機械装置重量とCO2排出量の関係の検討:CO2排出量の簡易推計のために, 日本LCA学会誌, 2008, 4 巻, 4 号, p. 349-358



“#234 石川ら(2008)の追試験” に対して3件のコメントがあります。