#247 重量単価の変化率を設定する
前回の投稿において、重量単価の最適化の効果を検証しました。検証の結果、重量単価の変化率において、先行研究である橘ら(2012)では大部分の品目が0.5倍から2倍の範囲であるのに対して、本研究では、0.5倍より小さい、もしくは2倍を超える品目が多く見られました。
その原因として、すべての品目において変化率上限・下限を± 0.7に設定したことが挙げられます。
そこで、今回の投稿では、変化率上限・下限を一律ではなく、品目ごとに設定する方法について検討を行いました。
橘ら(2012)における変化率上限・下限の設定
橘ら(2012)は、変化率上限・下限の設定について、以下のように言及しています。
変化率上限・下限としては,± 0.7 を限度とし,± 0.5,± 0.2,0 の値を,各品目の初期重量単価の信頼性などを基準に設定した。
けれども、橘ら(2012)の論文において、設定基準の詳細についての記述は見当たりません。
そこで、本研究では、生産量の統計値を推算する際に導入した「補正係数」を基準に、各品目の変化率上限・下限を設定します。
補正係数とは
投稿#243において、品目別国内生産額表に記載されている細品目を対象として、生産量を収集・積み上げ、平成12年産業連関表統合小分類の生産量を推計しました。同時に生産額についても積み上げ算定しました。
その際、品目別国内生産額表の細品目を産業部門ごとに積み上げた生産額は、必ずしも産業連関表の生産額と等しくなりません。
そこで、吉田ら(2006)が提唱する補正係数を用いて生産量を補正することにしました。
細品目を産業部門ごとに積み上げた生産額は必ずしも産業連関表に表示されている生産額と等しくならない。(中略)過不足が生じる場合には、次式(1)により生産量を補正した。産業連関表の生産額を基準として 、積み上げ生産額との比を補正係数として生産量を補正した。
$$
{YP^S}_i = {α^S}_i ✕ {YP^{SC}}_i
$$
$$
{YP^S}_i : i産業の域内生産量
$$
$$
{YP^{SC}}_i : i産業の積み上げた域内生産量(作成データ)
$$
統計調査に基づく(積み上げ)産業別生産額と滋賀県産業連関表の産業別生産額の比を ( α_i^S ) とすると、 生産量は式(2)で表される。
$$
{α^S}_i = \frac{{YM^{SI}}_i}{{YM^{SC}}_i}
$$
$$
{YM^{SI}}_i : i産業の域内生産額(産業連関表)
$$
$$
{YM^{SC}}_i : i産業の積み上げた域内生産額(作成データ)
$$
本研究では、式(1)および(2)の「域内」を「国内」という用語に置き換えて、補正係数αを導入することにしました。
本研究における変化率の上限・下限の設定方法
補正係数αは、初期重量単価の推計方法と関連しています。初期重量単価の推計方法は、以下のように整理することができます。
品目別国内生産額表から各品目の生産単位、生産数量、生産額のデータを引用し、各品目の初期重量単価を以下の手順で推計しました。
- 品目内製品の生産単位が全て重量表示の場合、それらの値を用いて算出。
- 品目内製品の生産単位の一部が重量表示の場合、その一部のみを用いて1. と同様に推計
- 品目内製品の生産単位に一つも重量表示が含まれないが、重量換算値が既存の統計資料から得られる場合、その重量換算値を用いて重量に換算
- 品目内製品の生産単位に一つも重量表示が含まれず、重量換算値が既存の統計資料を得ることが困難な場合、全国貨物純流動調査(物流センサス)の出荷原単位を用いて重量単価を算出
- 既に推計が完了している他の類似の産業と重量単価が同等と仮定して推計
- より大きい分類の平均重量単価を利用
- 産出物の材料となる投入物の重量を推計
- 物量表の値を利用
- 品目の産出がないため重量単価を設定しない
1.の場合は、補正係数αが1となり、品目別国内生産額表から生産量の統計値と初期重量単価の両方が推算できるため、変化率上限・下限の値を0に設定します。
2.および3.の場合、補正係数αの値によって、変化率上限・下限の値を、± 0.2, ± 0.5,± 0.7の3通りに設定します。吉田ら(2006)は、α>2.0の条件について、以下のように言及しています。
統計に基づく積み上げ域内生産額と産業連関表の域内生産額が大きく乖離していると判断される場合である。
本研究では、1<α<=2.0の場合は変化率の上限・下限を± 0.2に、2.0<α<=3.0の場合は変化率上限・下限を± 0.5に、α>3.0の場合は、変化率の上限・下限を± 0.7に設定することにします。
3.において品目内製品の全てが重量に換算できた場合および4.〜7.の方法で初期重量単価を推計した品目については、変化率上限・下限の値を± 0.2に設定します。
8.の場合は、補正係数が1となり、物量表から生産量の統計値と初期重量単価の両方が推算できるため、変化率上限・下限の値を0に設定します。
初期重量単価の推計方法と補正係数、変化率上限・下限の値の関係をまとめると、表247-1のようになります。
表247-1 初期重量単価の推計方法および補正係数と変化率の上限・下限の関係
| 初期重量単価の推計方法 | 補正係数α | 変化率の上限・下限 |
|---|---|---|
| 1, 8 | α=1 | 0 |
| 2, 3 | 1<α<=2 | ± 0.2 |
| 2, 3 | 2<α<=3 | ± 0.5 |
| 2, 3 | α>3 | ± 0.7 |
| 3, 4, 5, 6, 7 | - | ± 0.2 |
最適化の前後における生産量・廃棄物量の統計値と計算値
図247−1は、最適化の前後における生産量・廃棄物量の統計値と計算値の散布図になります。図の上部が初期重量単価を用いた場合の結果で、図の下部が上記の変化率上限・下限の設定で重量単価の最適化を行った場合の結果になります。
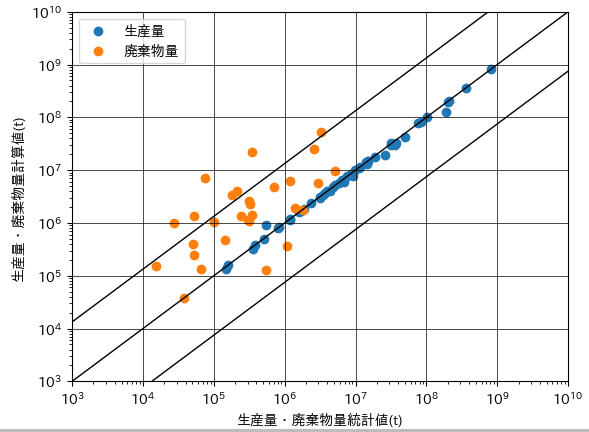
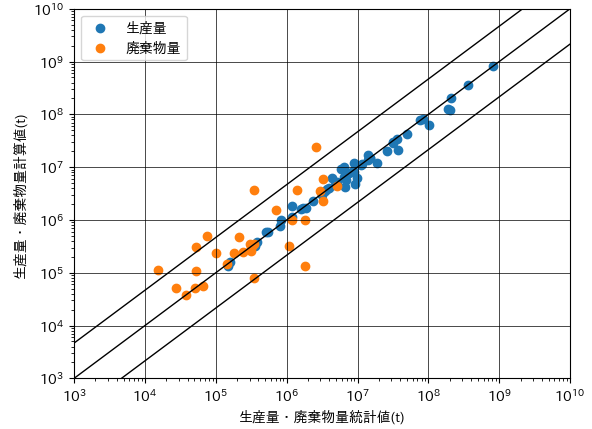
図247-1 生産量・廃棄物量の統計値と計算値(上)重量単価最適化前, (下)重量単価最適化後
初期重量単価を用いた場合においては,統計値と計算値が 10 倍以上異なる品目が
多く見られます。それに対して,最適化後の場合においては,大部分の品目が対角線付近に分布しており,良好な一致が見られたと言えます。なお,対角線の上下に描かれた直線は,相対差の標準偏差を示します。
最適化前後におけるMAPE
最適化前後における生産量・廃棄物量の統計値と計算値のMAPE(Mean of Absolute Percentage:平均絶対パーセント誤差)を下式によって算出しました。
$$
MAPE = \frac{1}{N}\sum_{i=1}^{n}\left|\frac{計算値_i - 統計値_i}{統計値_i}\right|
$$
ここで,N は対象となる品目の数,計算値は産業連関表から推算された生産量・廃棄物量,統計値は他の統計資料による値である。MAPE の値が小さいほど良好な結果であることを示し,計算値と統計値が完全に一致している場合には MAPE は0となる。
橘ら(2012)より引用
MAPEの値は、初期重量単価においては5.05で、最適化後においては1.75というように、値が小さくなったので、良好な結果が得られたと言えます。
MFA関連の4指標における比較
次に、マテリアルフロー分析(Material Flow Analysis:MFA)に関連する4つの指標(資源生産性、循環利用率、国内天然資源量、移輸入天然資源量)を計算しました。
MFAに関連する4つの指標の計算に先駆け、2000年産業連関表の取引金額に重量単価を乗じて、取引額を取引物量に変換した物量表を作成します。
資源生産性
資源生産性の計算には、2000年基準の実質GDPを用いました。資源生産性の計算式は、下記のようになります。
$$
資源生産性(万円/t) = \frac{GDP}{天然資源等投入量}
$$
計算式の分母にある天然資源等投入量は、以下の式から算出しました。
$$
天然資源等投入量 = 国内天然資源量 + 移輸入天然資源量
$$
国内天然資源量、移輸入天然資源量の計算方法については、後述します。
循環利用率
循環利用率の計算においては、循環利用量の値が必要となります。橘ら(2012)の論文において、循環利用量を推計方法についての記述を見つけることができませんでした。
そこで、本研究では、循環利用量の値として、環境統計集に記載の2000年の循環利用量(2.13億トン)を利用して、下記の定義式から循環利用率を算出しました。
$$
循環利用率 = \frac{循環利用量}{\;循環利用量 + 天然資源等投入量\;} × 100
$$
国内天然資源量
物量表の各項目における国内で産出される天然資源の合計値になります。
移輸入天然資源量
物量表の各項目における輸入資源と輸入製品の合計値になります。
上述の方法で計算した4つの指標の値を、環境統計集に記載されている2000年(平成12年)におけるそれらの値との間で比較した結果を表247-2に示します。
表247−2 最適化前後の資源生産性、循環利用率、国内天然資源量、移輸入天然資源量
| 最適化前 | 最適化後 | 環境統計集 | |
|---|---|---|---|
| 資源生産性(万円/t) | 24.18(-13.95%) | 25.29(-10.0%) | 28.10 |
| 循環利用率(%) | 8.71(−12.90%) | 9.07(-9.3%) | 10.00 |
| 国内天然資源量(億トン) | 12.52(11.28%) | 11.98(6.46%) | 11.25 |
| 移輸入天然資源量(億トン) | 8.95(19.19%) | 8.56(13.87%) | 7.52 |
重量単価の最適化前と後を比較すると大きな改善はないものの、15%以内の差で再現されていて、概ね良好な結果であると言えます。
重量単価の変化率の比較
最適化における2000年の重量単価の変化率について、橘ら(2012)と比較を行ったものが、図247-2になります。
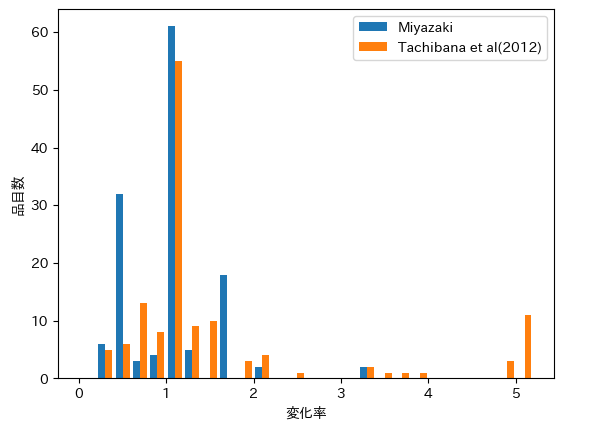
図247−2 重量単価変化率の度数分布
本研究(図247−2における「Miyazaki」)においては、すべての品目の重量単価変化率が0.2倍から3.4倍の範囲に収まっています。それに対して、橘ら(2012)においては、すべての品目の重量単価変化率が0.2倍から5倍の範囲でした。
また、本研究においても、橘ら(2012)においても、大部分の品目の重量単価変化率が0.5倍から2倍の範囲に収まっています。
橘ら(2012)は、大部分の品目において重量単価変化率が0.5倍から2倍の範囲であったことを受けて、以下のように言及しています。
初期重量単価の設定がある程度適切であったことを意味していると同時に,最適化後の重量単価の値についても妥当性が高いことを示唆している。
本研究においては、橘ら(2012)と比較して、重量単価変化率の最大値が小さく、重量単価変化率が0.6倍の品目数が多くなっています。
その原因として、初期重量単価の設定が比較的大きくなっていたことが挙げられます。
また、橘ら(2012)と同様に、大部分の品目において重量単価変化率が0.5倍から2倍の範囲であることから、最適化後の重量単価の値について妥当性が高いことを示唆していると考えます。



“#247 重量単価の変化率を設定する” に対して1件のコメントがあります。