#249 重量単価の変化率を設定する(その2)
前回の投稿において、最適化によって得られた重量単価を用いて、神奈川県のマテリアルフローを推計しました。その結果、重量単価の妥当性が低いことが判明しました。その原因の一つして、最適化計算における重量単価変化率の設定が適切でないことを挙げました。
今回の投稿では、最適化計算における重量単価変化率の設定について、2回目の検討を行います。
比較表の作成
先行研究である橘ら(2012)の初期重量単価、最適化後の重量単価および本研究における初期重量単価の3つの値を比較することで、最適化計算における重量単価の変化率を検討することにしました。
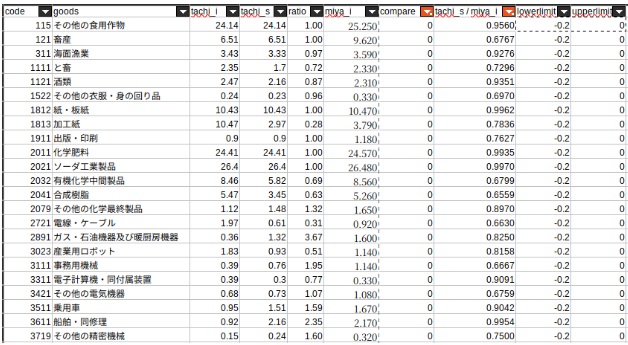
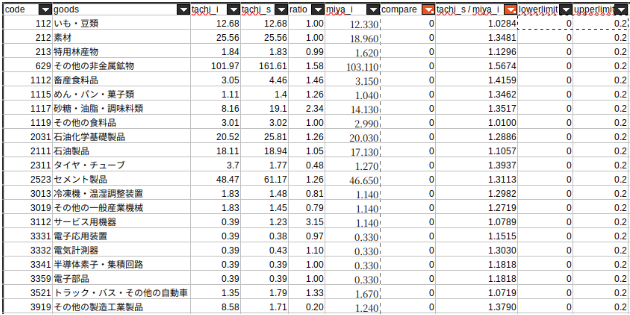
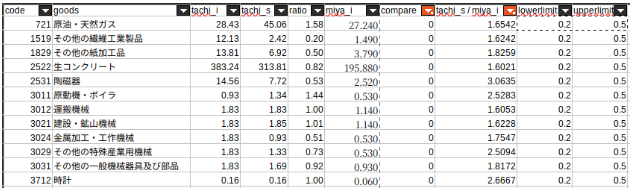
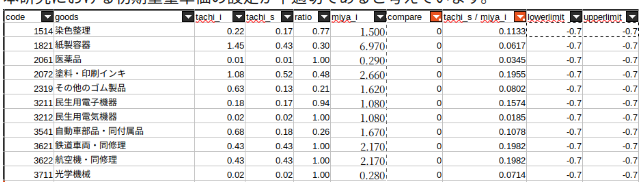
比較表における列名の説明は、下記のようになります。
列名の説明
- tachi_i:橘ら(2012)における初期重量単価(t/百万円)
- tachi_s:橘ら(2012)における最適化後の重量単価(t/百万円)
- ratio:橘ら(2012)における最適化後の重量単価を橘ら(2012)における初期重量単価で除した値。
- miya_i:本研究における初期重量単価(t/百万円)
- compare:本研究における初期重量単価が橘ら(2012)における初期重量単価と等しいかどうかの真偽値。等しい場合は1、等しくない場合は0。
- miya_i / tachi_s : 本研究における初期重量単価を橘ら(2012)における最適化後の重量単価で除した値。
- lowerlimit:変化率下限の設定値
- upperlimit:変化率上限の設定値
次に、compareの値、ratioの値およびmiya_i / tachi_sの値によって場合分けを行い、それぞれの場合における変化率の上限・下限について検討を行いました。
まず、(1)compareの値が1(本研究における初期重量単価が橘ら(2012)における初期重量単価と等しい)と、(2)compareの値が0(本研究における初期重量単価が橘ら(2012)と異なる)の2つに大別しました。
そして、(1)においては、ratio(橘ら(2012)における最適化後の重量単価を橘ら(2012)における初期重量単価で除したもの)の値によって、(2)においては、miya_i / tachi_s(本研究における初期重量単価を橘ら(2012)における最適化後の重量単価で除したもの)の値によって、さらに場合分けを行いました。
(1)本研究における初期重量単価が橘ら(2012)における初期重量単価と等しい場合
ratio = 1
変化率下限・上限を0に設定
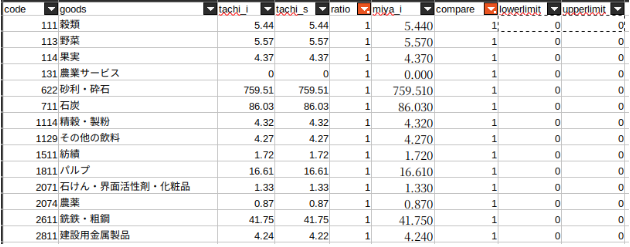
橘ら(2012)において10^-0.7 <= ratio < 10^-0.5
変化率の下限を-0.7、上限を-0.5に設定

橘ら(2012)において10^-0.5 <= ratio < 10^-0.2
変化率下限を-0.5、上限を-0.2に設定

橘ら(2012)において10^-0.2 <= ratio < 1の場合
変化率下限を-0.2、上限を0に設定

橘ら(2012)において 1 < ratio < 10^0.2の場合
変化率下限を0、上限を0.2に設定

橘ら(2012)において 10^0.2 <= ratio <= 10^0.5の場合
変化率下限を0.2、上限を0.5を0に設定

橘ら(2012)において ratio > 10^0.5の場合
該当産業なし
(2)本研究の初期重量単価が橘ら(2012)における初期重量単価と異なる場合
10^-0.7倍 > 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価
変化率下限を-0.7、上限を-0.7に設定。
尚、このケースに該当する産業においては、本研究における初期重量単価の設定が不適切であると考えています。
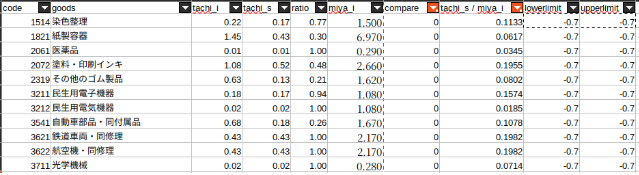
10^-0.7倍 <= 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価 < 10^-0.5倍
変化率下限を-0.7、上限を-0.5に設定
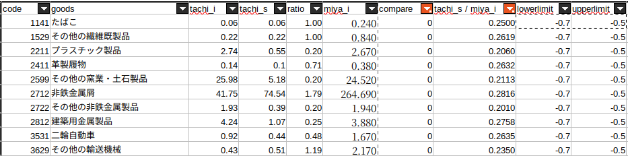
10^-0.5倍 <= 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価 < 10^-0.2倍
変化率下限を-0.5、上限を-0.2に設定
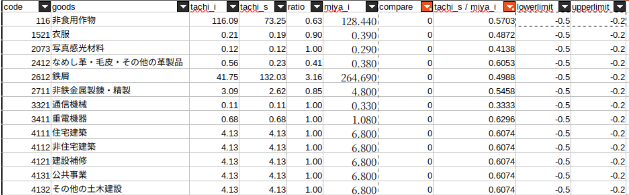
10^-0.2倍 <= 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価 < 1倍
変化率下限を-0.2、上限を0に設定
1 < 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価 < 10^0.2倍
変化率下限を0、上限を0.2に設定
10^0.2倍 <= 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価 < 10^0.5倍
変化率下限を0.2、上限を0.5に設定
10^0.5倍 <= 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価 < 10^0.7倍
変化率下限を0.5、上限を0.7に設定

10^0.7倍 <= 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価
変化率下限を0.7、上限を0.7に設定
尚、このケースに該当する産業においては、本研究における初期重量単価の設定が不適切であると考えています。

重量単価の最適化を実行
上述の変化率上限・下限の設定のもと、重量単価の最適化計算を実行しました。
図249−1は、最適化前後における生産量・廃棄物量の統計値と計算値の散布図になります。
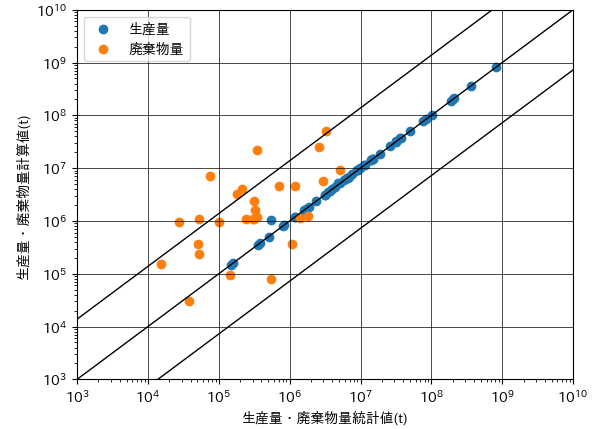
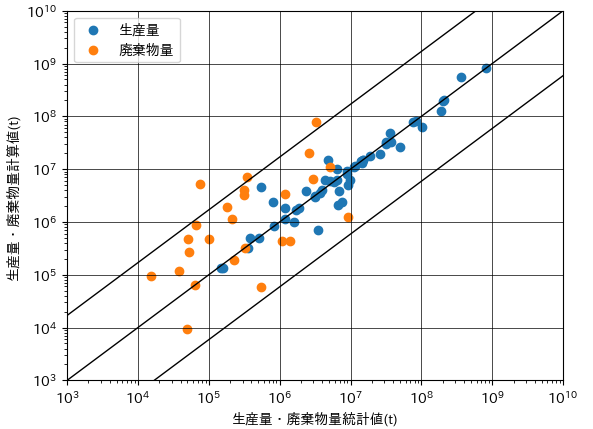
図249−1 生産量・廃棄物量の統計値と計算値(上)重量単価最適化前、(下)重量単価最適化後
最適化計算によって、統計値と計算値が10倍以上異なる品目が増えました。また、相対差の標準偏差を表す、対角線の上下に描かれた2本の直線の幅が広がりました。
生産量・廃棄物量の統計値と計算値のMAPE(Mean of Absolute Percentage Error:相対差の絶対値の平均)を計算すると、最適化前の値が5.11であるのに対して、最適後の値は6.20と大きくなりました。
MAPEの値が小さいほど、統計値と計算値が一致度合いが高いことを示すので、最適化計算によって統計値と計算値が離れてしまったことが示唆されます。
統計値と計算値が離れてしまった原因について、検討を行います。
生産量の統計値は、投稿#243で言及している方法を用いて推算を行っています。
まず、品目別国内生産額表に記載されている細品目を対象として、生産量を収集・積み上げると同時に生産額についても積み上げ算定しました。
その際、品目別国内生産額表の細品目を産業部門ごとに積み上げた生産額は、必ずしも産業連関表の生産額と等しくなりません。そこで、以下に定義する補正係数を用いて生産量を補正することにしました。
$$
{YP^S}_i = {α^S}_i ✕ {YP^{SC}}_i
$$
$$
{YP^S}_i : i産業の国内生産量
$$
$$
{YP^{SC}}_i : i産業の積み上げた国内生産量(作成データ)
$$
$$
{α^S}_i = \frac{{YM^{SI}}_i}{{YM^{SC}}_i}
$$
$$
{YM^{SI}}_i : i産業の国内生産額(産業連関表)
$$
$$
{YM^{SC}}_i : i産業の積み上げた国内生産額(作成データ)
$$
また、補正係数が2を超える場合、品目別国内生産額表を元に生産量を推算することが不可能と判断し、生産量の統計値を推算していません。
すなわち、補正係数が2以下の産業については、積み上げた国内生産額に補正係数を乗じると、国内生産額と等しくなります。すなわち、推算した国内生産量(統計値)が、産業連関表の国内生産額に初期重量単価を乗じた値(計算値)と等しくなり、これらの産業では、図249−1の上部における対角線上にプロットされています。
ところが、最適化計算において、図249−1の上部における対角線上にプロットされた産業の中には、変化率上限および下限が1以外の値に設定されて、対角線から離れていくものが出現します。生産量の統計値と計算値が離れたことで、MAPEが最適化前に比べて大きくなったと考えています。
最適化によって、統計値と計算値がより離れてしまったわけですが、橘ら(2012)の初期重量単価におけるMAPEの値(22.52)に比べれば、最適化後のMAPEの値(6.20)は小さくなっています。
MFAに関連する4つの指標
次に、MFA(Material Flow Analysis : マテリアルフロー分析)に関連する4つの値(資源生産性、循環利用率、国内天然資源量、移輸入天然資源量)を計算し、環境統計集に記載されているそれらの値との間で比較しました。
表249-1 最適化前後の資源生産性、循環利用率、国内天然資源量、移輸入天然資源量
| 最適化前 | 最適化後 | 環境統計集 | |
|---|---|---|---|
| 資源生産性(万円/t) | 30.49(8.51%) | 29.3(4.27%) | 28.10 |
| 循環利用率(%) | 10.74(7.4%) | 10.36(3.60%) | 10.00 |
| 国内天然資源量(億トン) | 12.43(10.51%) | 11.71(4.10%) | 11.25 |
| 移輸入天然資源量(億トン) | 4.43(-41.15%) | 5.36(-28.75%) | 7.52 |
最適化によって、各指標とも改善が見られました。
本投稿で得られた重量単価を用いて、2000年神奈川県のMFAを行いました。橘ら(2012)が最適化した重量単価を用いて推計した2000年の神奈川県のマテリアルフローは図249-2のようになります。
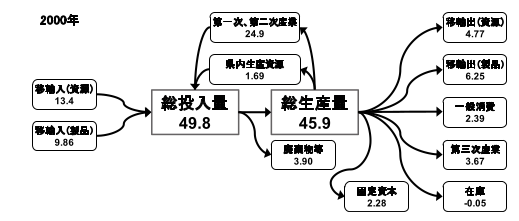
図249−2 神奈川県の生産活動における2000 年のマテリアルフロー(単位:t/ 人 / 年)(橘ら(2012)より一部を引用)
本研究の最適化前後および橘ら(2012)における神奈川県のマテリアルフローの各項目の値を比較すると、表249-2のようになります。
表249−2 本研究の最適化前後およびと橘ら(2012)における神奈川県マテリアルフローの各項目値
| 最適化前 | 最適化後 | 橘ら(2012) | |
|---|---|---|---|
| 移輸入(資源) | 12.63(-5.75%) | 14.07(5.00%) | 13.40 |
| 移輸入(製品) | 5.66(-42.60%) | 6.72(-31.85%) | 9.86 |
| 県内生産資源 | 0.98(-42.01%) | 1.12(-33.73%) | 1.69 |
| 第一次、第二次産業 | 21.27(-14.58%) | 23.15(-7.03%) | 24.90 |
| 総投入量 | 40.53(-18.61%) | 45.95(-7.73%) | 49.80 |
| 総生産量 | 50.70(10.46%) | 42.72(-6.93%) | 45.90 |
| 廃棄物等 | −8.17(-309.49%) | 4.12(5.64%) | 3.90 |
| 移輸出(資源) | 6.48(35.85%) | 5.73(20.13%) | 4.77 |
| 移輸出(製品) | 6.18(-1.12%) | 5.49(-12.16%) | 6.25 |
| 一般消費 | 1.65(-30.96%) | 2.11(-11.72%) | 2.39 |
| 第三次産業 | 4.00(3.36%) | 3.35(-13.44%) | 3.87 |
| 在庫 | 0.00(-100.00%) | −0.01(-80.00%) | -0.05 |
| 固定資本 | 10.15(345.18%) | 1.77(-22.37%) | 2.28 |
移輸出(製品)および第三次産業では、最適化後の値が最適前の値に比べて、橘ら(2012)の値から離れてしまいましたが、それら以外の項目においては、最適化後の値が、橘ら(2012)の値に近くなりました。
最適化後においても、移輸入(製品)や県内生産資源、在庫の値が橘ら(2012)における値から離れているのが気になります。
そこで、本研究における初期重量単価の設定が不適切であると考える産業、すなわち、
- 0^-0.7倍 > 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価:変化率下限を-0.7、上限を-0.7に設定した産業
- 10^0.7倍 <= 橘ら(2012)における最適化後の重量単価 / 本研究における初期重量単価 :変化率下限を0.7、上限を0.7に設定に設定した産業

について、初期重量単価を橘ら(2012)と等しくと仮定し、変化率上限・下限を橘ら(2012)と同じに設定した上で、再度最適化することを次回の投稿で試みることにします。



“#249 重量単価の変化率を設定する(その2)” に対して1件のコメントがあります。