#246 重量単価の最適化の効果を検証
前回の投稿では、生産量・廃棄物量の統計値と計算値が最小となるように、初期重量単価の最適化を行いました。今回の投稿は、重量単価の最適化の効果を検証します。
最適化前後における生産量・廃棄物量の統計値と計算値
図246-1に、最適化前後における生産量・廃棄物量の統計値と計算値の散布図を示します。上が初期重量単価を用いた場合の結果であり、下が最適化計算によって重量単価の設定を行った場合の結果です。
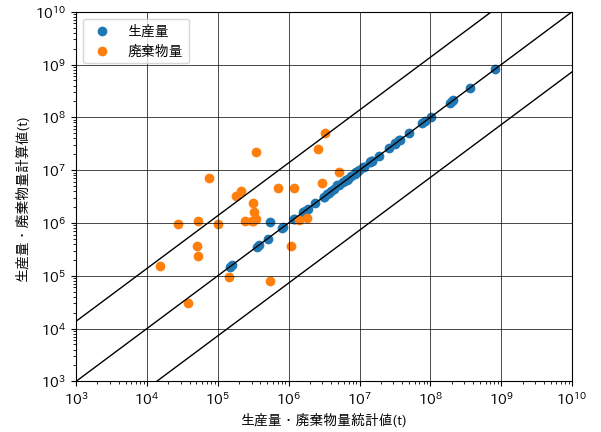
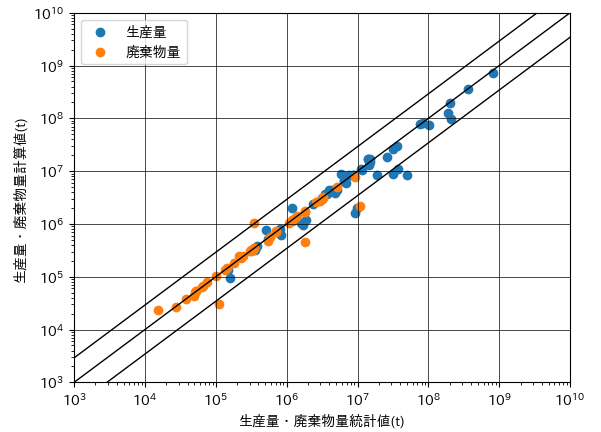
図246−1 生産量・廃棄物量の統計値と計算値(上)重量単価最適化前, (下)重量単価最適化後
初期重量単価を用いた結果においては、統計値と計算値が10倍以上異なる品目が多く見られるのに対して、最適化後の結果においては、大部分の品目が対角線付近に分布していて、良好な一致が見られたと言えます。
なお、対角線の上下に描かれた直線は、相対誤差の標準偏差を表しています。
最適化前後におけるMAPE
最適化前後における生産量・廃棄物量の統計値と計算値のMAPE(Mean of Absolute Percentage:平均絶対パーセント誤差)を下式によって算出しました。
$$
MAPE = \frac{1}{N}\sum_{i=1}^{n}\left|\frac{計算値_i - 統計値_i}{統計値_i}\right|
$$
ここで,N は対象となる品目の数,計算値は産業連関表から推算された生産量・廃棄物量,統計値は他の統計資料による値である。MAPE の値が小さいほど良好な結果であることを示し,計算値と統計値が完全に一致している場合には MAPE は0となる。
橘ら(2012)より引用
MAPEの値は、初期重量単価においては 5.05 5.06(2024年6月30日訂正)で、最適化後においては0.27 0.18(2024年6月30日訂正)というように、値が小さくなったので、良好な結果が得られたと言えます。
MFA関連の4指標における比較
次に、マテリアルフロー分析(Material Flow Analysis:MFA)に関連する4つの指標(資源生産性、循環利用率、国内天然資源量、移輸入天然資源量)を計算しました。
MFAに関連する4つの指標の計算に先駆け、2000年産業連関表の取引金額に重量単価を乗じて、取引額を取引物量に変換した物量表を作成します。
資源生産性
資源生産性の計算には、2000年基準の実質GDPを用いました。資源生産性の計算式は、下記のようになります。
$$
資源生産性(万円/t) = \frac{GDP}{天然資源等投入量}
$$
計算式の分母にある天然資源等投入量は、以下の式から算出しました。
$$
天然資源等投入量 = 国内天然資源量 + 移輸入天然資源量
$$
国内天然資源量、移輸入天然資源量の計算方法については、後述します。
循環利用率
循環利用率の計算においては、循環利用量の値が必要となります。橘ら(2012)の論文において、循環利用量を推計方法についての記述を見つけることができませんでした。
そこで、本研究では、循環利用量の値として、環境統計集に記載の2000年の循環利用量(2.13億トン)を利用して、下記の定義式から循環利用率を算出しました。
$$
循環利用率 = \frac{循環利用量}{\;循環利用量 + 天然資源等投入量\;} × 100
$$
国内天然資源量
物量表の各項目における国内で産出される天然資源の合計値になります。
移輸入天然資源量
物量表の各項目における輸入資源と輸入製品の合計値になります。
上述の方法で計算した4つの指標の値を、環境統計集に記載されている2000年(平成12年)におけるそれらの値との間で比較した結果を表246-1に示します。
表246−1 最適化前後の資源生産性、循環利用率、国内天然資源量、移輸入天然資源量
| 最適化前 | 最適化後 | 環境統計集 | |
|---|---|---|---|
| 資源生産性(万円/t) | 24.18(-13.95%) | 28.8万円(2.49%) | 28.10 |
| 循環利用率(%) | 8.71(-12.9%) | 10.2(2.00%) | 10.00 |
| 国内天然資源量(億トン) | 12.52(11.28%) | 9.73(-13.55%) | 11.25 |
| 移輸入天然資源量(億トン) | 8.96(19.19%) | 8.34(10.96%) | 7.52 |
最適化前に比べて、最適化後では、4つの指標のすべてにおいて環境統計集の値からかけ離れる結果となりました国内天然資源料については値が環境統計集から離れてしまいましたが、それ以外の指標において改善が見られました。4つの指標全てにおいて、環境統計集との差が15%以内に収まったので、概ね良好な結果が得られたと言えます。
(2024年6月30日訂正と追記、追記箇所は太字の部分)
重量単価の変化率の比較
MFAに関連する4つの指標の値が、環境統計集のそれらの値から大きくかけ離れた原因を探るために、重量単価の変化率を見てみることにしました。
(2024年6月30日削除)
最適化における2000年の各重量単価の変化率について、橘ら(2012)と比較を行ったものが、図246−2になります。
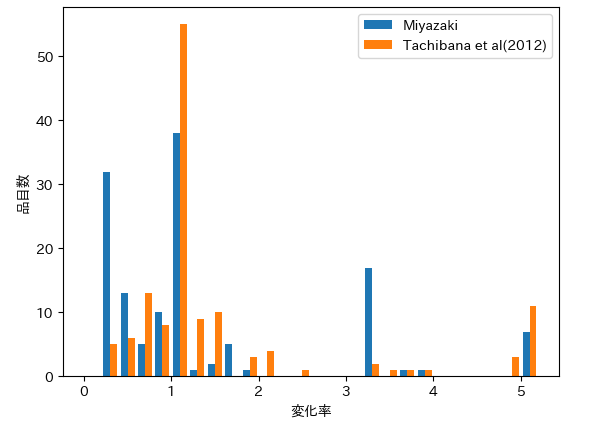
図246−2 重量単価変化率の度数分布
本研究(図246−2における「Miyazaki」)でも橘ら(2012)でも、すべての重量単価の変化率が0.2倍から5倍の範囲でした。
橘ら(2012)では大部分の品目において、0.5倍から2倍の範囲に収まっています。
対して、本研究では、0.5倍より小さい、または2倍を超える範囲に多くの品目があります。
橘ら(2012)は、各品目の変化率上限・下限を以下のように設定しています。
変化率上限・下限としては,± 0.7 を限度とし,± 0.5,± 0.2,0 の値を,各品目の初期重量単価の信頼性などを基準に設定した。
橘ら(2012)より引用。
一方、本研究では、変化率上限・下限を品目ごとに設定せず、一律に± 0.7に設定しています。
そこで、次回の投稿では、変化率上限・下限を品目ごとに検討していきたいと考えています。



“#246 重量単価の最適化の効果を検証” に対して1件のコメントがあります。