#244　初期重量単価における2000年の生産量・廃棄物量の統計値と計算値

前回の投稿では、品目別国内生産額表をもとに生産量を推算することおよび補正係数による推算の補正について言及しました。この度、生産量の推算（統計値）が完了しました。

今回の投稿は、初期重量単価における生産量・廃棄物量の統計値と計算値の乖離度合いについて視覚化、定量化についてです。

初期重量単価における生産量・廃棄物量の統計値と計算値の散布図

図244−1は、本研究での初期重量単価における生産量・廃棄物量の統計値と計算値の散布図を示します。

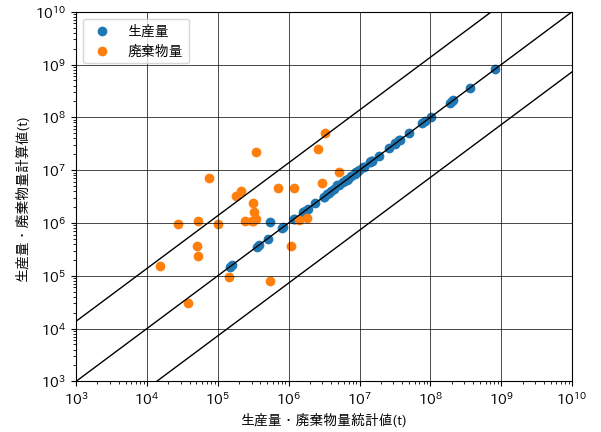
図244-1　本研究での初期重量単価における生産量・廃棄物量の統計値と計算値

生産量については、大部分の品目が対角線付近に分布しているのに対して、廃棄物量については、統計値と計算値が10倍以上異なる品目が多く見られます。なお、対角線の上下に描かれた直線は、相対誤差の標準偏差を表しています。

図244-2は、橘ら（2012）による重量単価の最適化前後における生産量・廃棄物量の統計値と計算値の散布図を示します。

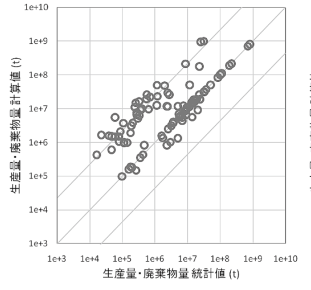
図244-2　橘ら（2012）による生産量・廃棄物量の統計値と計算値（重量単価最適化前）（橘ら（2012）より一部引用）

橘ら（2012）では、生産量と廃棄物量のプロットを区別していませんが、最適化前において統計値と計算値が10倍以上異なる品目が多く見られる点が本研究と一致しています。

MAPEによる統計値と計算値の一致度合いの定量化

橘ら（2012）は、これらの結果を定量的に評価するために、生産量・廃棄物量の統計値と計算値のMAPE(Mean of Absolute Percentage Error：相対差の絶対値の平均)を、下式によって算出しています。

$$
MAPE = \frac{1}{N}\sum_{i=1}^{n}\left|\frac{計算値_i - 統計値_i}{統計値_i}\right|
$$

ここで，N は対象となる品目の数，計算値は産業連関表から推算された生産量・廃棄物量，統計値は他の統計資料による値である。MAPE の値が小さいほど良好な結果であることを示し，計算値と統計値が完全に一致している場合には MAPE は０となる。

本研究でのMAPEの値は、4.78 5.07（2024年6月30日訂正）となりました。橘ら（2012）では、22.52でした。初期重量単価において、橘ら（2012）よりもMAPEの値が小さくなったのは、驚きでした。と同時に、本研究のどこかに間違いがあるような気がしていることも事実です。

引用文献

• 橘 隆一, 近藤 浩正, 荒川 正幹, 後藤 尚弘, 船津 公人, 藤江 幸一, 産業連関表を用いた重量単価の最適化モデルの開発と神奈川県のマテリアルフロー分析への応用, 環境科学会誌, 2012, 25 巻, 2 号, p. 134-150

Follow me!